Inverting a binary tree using x64 assembly

While browsing twitter, I came across this tweet:

Some ground rules

The task is to invert a binary tree. A binary tree node is defined as follows:

struct TreeNode{ 
    int val;
    struct TreeNode * left;
    struct Treenode * right;
};

This definition is from Leetcode 226. After we are done, we can submit our code there to see if it works.

I will be using x64 assembly with the AT&T syntax as it is objectively superior than the Intel syntax.

Technically the tweet asks to invert a merkle tree, however you can easily extend the final code to recompute the hash at each node after its two subtrees are inverted.

Pseudocode

The function we need to implement is as follows:

struct TreeNode * invertTree(struct TreeNode * root);

We will begin by writing some pseudocode

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

function invert(root) {
    let local_root = root;
    if local_root is null {
        return null
    }

    let local_left = local_root.left;
    let local_right = local_root.right;

    root.right = invert(local_left);
    root.left = invert(local_right);

    return local_root;
}

This pseudocode is intentionally verbose so we can easily track all local variables we have to create and store on the stack. We will be translating this pseudocode as it is to assembly.

Basic setup

1
2
3
4
5

.globl invert_tree
.type invert_tree, @function
.section .text
invert_tree:
    # Our function goes here

Lines 1 and 2 tell the assembler that we are defining an invert_tree symbol of type function. The globl modifier allows our function to be called from other source files. The .text section is the Code segment where we will be writing our function.

Function prologue and epilogue

To define this function in assembly, we first need to understand the x86-64 calling convention. This is documented in the System V ABI available here.

1
2
3
4
5
6
7
8
9

invert_tree:
    # Function prologue
    push %rbp
    mov %rsp, %rbp
    sub $32, %rsp

    # Function epilogue
    leave
    ret

First, we push the current value of %rbp on the stack and copy %rsp to %rbp. We then subtract 32 bytes from the stack pointer to make space to store our local variables.

Doing this sets up a stack frame for this function, with %rbp as the “base”. We can now use offsets from %rbp to access data on the stack.

There is an enter instruction which sets up the stack frame for us, but it is very slow. On modern processors enter decodes to some 10 to 20 µops, while the three instruction sequence is about 4 to 6, depending on the architecture. Source

The leave instruction does exactly the opposite of lines 3 and 4. It restores %rsp and pops the value from stack into %rbp.

Stack alignment

In our pseudocode, there are 3 local variables local_root, local_left and local_right. Each of these is a pointer type, thus they require a total of 24 bytes to be stored on the stack (A pointer type has size 8 bytes in x64).

However, we instead make space for 32 bytes to ensure our stack is “aligned” correctly. From the System V ABI document:

“The stack needs to be 16 byte aligned immediately before any call instruction is executed.”

Base case

The function accepts a single pointer as input, thus according to the calling convention, we will be receiving it as a 64 bit value in the register %rdi.

To return a pointer from our function, we have to store it in the register %rax before we ret from our function.

We check if the root is NULL, and if it is, we return NULL.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

invert_tree:
    # Function prologue
    push %rbp
    mov %rsp, %rbp
    sub $32, %rsp

    # --------- Base case ---------
    # %rdi contains the input parameter (8 byte pointer to the root)
    cmp $0, %rdi
    # Root not NULL, continue with execution
    jne continue
    # Root is NULL, store NULL in %rax and return
    xor %rax, %rax
    jmp done
continue:

done:
    # Function epilogue
    leave
    ret

In x64, NULL is the value 0. We compare %rdi with 0 and if it succeeds, we put 0 in %rax and return from our function. To do this, using xor is faster than mov or sub.

Struct alignment

On most ISA’s each data type in a struct has an alignment requirement. What this means is that the address of a type must start on an address which is a multiple of their size. (There are some exceptions, but this is the general rule)

So int’s must start on an address which is a multiple of 4, and pointers must start on an address which is a multiple of 8.

Given this, our original struct is laid out in memory something like so:

struct TreeNode{ 
    int val;
    char pad[4];  // 4 extra bytes to align the next pointer
    struct TreeNode * left;
    struct Treenode * right;
};

This wastes 4 bytes for every struct in memory. We can save this space by declaring the pointers first, however we will continue to use the original struct declaration as we want to submit this to Leetcode.

Storing local variables on the stack

Once we know the address offsets in our struct, we can then store them on the stack. We will store local_root, left and right pointers on the stack. Each of them has a size of 8 bytes. We store them as follows

Also, to make referring to them easier, we can define these offsets as constants using the equ assembler directive.

1
2
3
4
5
6
7
8

# ...
.section .text
.equ local_root, -8
.equ local_left, -16
.equ local_right, -24

invert_tree:
# ... function here

We can then use them in our code.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

invert_tree:
    # ...
continue:
    # --------- Save local variables to stack ---------
    # Save the root parameter as local_root on stack
    movq %rdi, local_root(%rbp)

    # Advance 8 bytes from root, to get left pointer in struct.
    movq 8(%rdi), %rdx
    # Store this as local_left to stack
    movq %rdx, local_left(%rbp)

    # Advance 16 bytes from root, to get to right pointer in struct.
    movq 16(%rdi), %rdx
    # Store this as local_right to stack
    movq %rdx, local_right(%rbp)

done:
    # ...

Do the recursive calls

At this point, looking at the pseudocode, we simply need to perform 2 recursive calls.

To do this, we store the correct parameter to %rdi and use the call instruction.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

invert_tree:
    # Function prologue
    push %rbp
    mov %rsp, %rbp
    sub $32, %rsp

    # --------- Base case ---------
    # %rdi contains the input parameter (8 byte pointer to the root)
    cmp $0, %rdi
    # Root not NULL, continue with execution
    jne continue
    # Root is NULL, store NULL in %rax and return
    xor %rax, %rax
    jmp done
continue:
    # --------- Save local variables to stack ---------
    # Save the root parameter as local_root on stack
    movq %rdi, local_root(%rbp)

    # Advance 8 bytes from root, to get left pointer in struct.
    movq 8(%rdi), %rdx
    # Store this as local_left to stack
    movq %rdx, local_left(%rbp)

    # Advance 16 bytes from root, to get to right pointer in struct.
    movq 16(%rdi), %rdx
    # Store this as local_right to stack
    movq %rdx, local_right(%rbp)

    # --------- Recursive calls ---------
    # Recursively call invert_tree on local_right
    movq local_right(%rbp), %rdi
    call invert_tree

    # Calculate address of root.left
    movq local_root(%rbp), %rdx
    addq $8, %rdx
    # Assign root.left to value returned from recursive call
    movq %rax, (%rdx)
    
    # Recursively call invert_tree on local_left
    movq local_left(%rbp), %rdi
    call invert_tree

    # Calculate address of root.right
    movq local_root(%rbp), %rdx
    addq $16, %rdx
    # Assign root.right to value returned from recursive call
    movq %rax, (%rdx)

    # Return root
    movq local_root(%rbp), %rax

done:
    # Function epilogue
    leave
    ret

To assign the results of the recursive calls, we use the %rdx register to compute the correct addresses of root.left and root.right. Most of this is a straight translation of the pseudocode.

Submitting to leetcode

We cannot submit assembly to Leetcode, so we will use C instead. Leetcode uses gcc to compile our code, so we can use the __asm__ directive to add our assembly.

We need to also declare our function with extern before we can call it.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

typedef struct TreeNode TreeNode;
extern TreeNode* invert_tree(TreeNode*);

__asm__(".global invert_tree  \n\t"
".type invert_tree, @function \n\t"
".section .text               \n\t"
// Rest of our code here...
);

// Leetcode func
TreeNode* invertTree(TreeNode* root){
    return invert_tree(root);
}

And we are done!

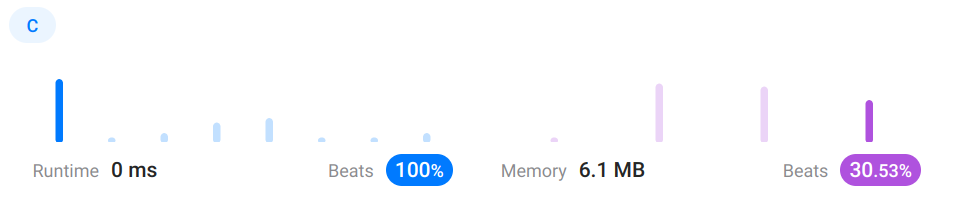
The leetcode performance and memory numbers are very unreliable, so we don’t really know how much faster our program is compared to other submissions, but I suspect it is pretty fast.

Conclusion

This was a fun excursion to brush up on my assembly skills. It wasn’t difficult, but definitely was tedious (This is generally how I feel about most leetcode style questions).

At least now I can relate to more memes on r/ProgrammerHumor

HN Front page update

People on HN and reddit found this post amusing.

Thanks for reading. Happy Thanksgiving!